I've always been passionate about computers and their potential impact on our daily lives... Whether through work, entertainment or how, most of what is around us is operated by some system, someone thought out.
Once you start seeing these things for what they are... You want to dig and understand more in depth... Yet it remains elusive because, well, technology is complicated. It usually involves maths, programming and a lot of trial and error.
I've also always been fascinated by automation, at 14 years old I was running multiple botted Instagram accounts that would have random intervals to like other people's images and they would come follow mine.
For this blog post I will go in detail of how to build an automated Snake game, it's a great example because the environment is relatively simple yet playing that game "well" is difficult.
We'll explore the evolution of an AI agent designed to play the classic game Snake. We'll start with a basic Q Table model, SNAIK, and progressively improve it through iterations, each introducing new concepts and techniques from machine learning and artificial intelligence. By the end, we'll have a neural network-based agent capable of playing Snake at a high level.
It took days, if not weeks to write, so I hope you enjoy!
So first let's set the basics of the game. Even though you already know it. For machine learning, it's important to have a full picture of what the environment is exactly.
The snake has a space of 960px / 640px. Broken into blocks of 20 pixels.
This means the game grid is effectively divided into:
48 blocks horizontally (960 / 20 = 48)
32 blocks vertically (640 / 20 = 32)
Now the snake is a growing line (starts with 3 blocks) continuously moving in a direction (can't do 180 turns) around a confined space (defined above^^), eating food, and avoiding collisions.
The challenge increases as the snake gets longer, requiring more careful navigation.
The goal of the game is simply to get to as high of a score as possible, but also in the least amount of tries.
This makes it a great medium for machine learning as we can use the score for the reward system and collisions as a punishment. This creates a balanced learning environment.
Let's call our system: SNAIK
Now for this first version of the code, we give no restraints to the system. Meaning it's able to perform actions that are humanly impossible, for example, pressing keys in split milliseconds with precision.
This is interesting because let's say that someone who likes games has a reaction time of 0.1 second, which is already pretty amazing. Our system, in this case, can perform up to 30 or probably even more actions, in one second. While the human counterpart, would have made 10, and he's incredibly fast!

Example of totally inhuman movement, as you can see with diagonal moves that would be impossible to replicate.
SNAIK still crashed at score 27 due to the fact that it lacked the ability to plan its own crazy moves, essentially trapping itself. Yet if you coded this perfectly you could probably get it to play the game perfect using a grid system but our aim is to not cheat and just give the same visual feedback we have to an agent and not hardcode a win.
Now let's create SNAIK2.
In this version we will use the shortest/longest path technique, and Breadth-First Search Algorithm. Essentially, BFS algorithm explores all possible neighbour nodes at the present level before moving to the next depth level, it uses FIFO data structure in a queue, treats each block as a node and neighbours as distance from the current node. This is our short paths to food.
In mathematical terms: All positions at distance k from the start are processed before any at distance k+1. Uses vectors in a 2d space (x + dx, y + dy).
Now we add a second-longest safe path technique, mixed with backtracking and collision checks, that is only called when the short path is invalid.

Examples at score 38-41, you can clearly see the use of the longest safe path/collision checking.
The rest of the time you can see the algo in action. You could run this to much higher scores.
def find_path(self, start, goal):
queue = deque([[start]])
visited = set([tuple(start)])
while queue:
path = queue.popleft()
pos = path[-1]
if pos == goal:
return path
for dx, dy in [(0, -BLOCK_SIZE), (0, BLOCK_SIZE), (-BLOCK_SIZE, 0), (BLOCK_SIZE, 0)]:
next_pos = [pos[0] + dx, pos[1] + dy]
if self.is_valid(next_pos) and tuple(next_pos) not in visited:
queue.append(path + [next_pos])
visited.add(tuple(next_pos))
return NoneIt ensures correct order of exploration, prevents redundant work and ensures termination when the goal is reached. This is cheating a hard-coded win.
Tuples in python are like a time capsule, once you write a position you can't change it... This is why it's especially relevant, it's a reliable way to "remember" temporal information. It's faster and more memory efficient than lists. Even more so, for time sensitive operations.
Now this is great and all... But it's not realistic...
We should implement a delay of human reactions. Let's set this number to 0.2 seconds. Meaning a maximum of 5 actions per second.
Let's call this version SNAIL aha!

You can observe how much harder it becomes for SNAIL to even get to 7 score.
I used https://humanbenchmark.com/tests/reactiontime as a baseline (273 ms is the average) but the peak is around 200 ms.
The bulk lies within 100ms to 450ms, which could be interesting to test on our AI.
Or we could use the range, which seems to be 150ms to 300ms.
We should also subtract 10 ms for hardware.
So now instead of a fixed 0.2, we will use 0.1 min, 0.45 max and 0.225 median.

You can observe that sometimes it will be much more precise and sometimes struggle, which makes sense due to our constraints. This gives us a solid contrast between inhuman reactions and simulated delay.
Now it's a bit unfair to SNAIL... Us humans, while limited in our reaction time, can also kind of try to plan ahead, so much so, we try to hit the right movement key just as the pixel is changing, this is "anticipation" or "pre-shooting". I made the test out of curiosity.
Time since last keypress: 201.925760 ms
Time since last keypress: 0.045166 ms
Time since last keypress: 605.687703 ms
Time since last keypress: 200.008360 ms
Time since last keypress: 1210.042729 ms
Time since last keypress: 101.043839 ms
Time since last keypress: 904.732755 ms
Time since last keypress: 202.607632 ms
Time since last keypress: 804.382054 ms
Time since last keypress: 100.465890 ms
Time since last keypress: 202.917760 ms
Time since last keypress: 99.857918 ms Out of 12 random moves, 4 are lower or close to 100ms and one is incredibly low at 0.045 ms. Some are also almost a full second or more.
So for our machine learning model we will need to take this in consideration, as we cannot simply use a 0.2 delay. Well, if you try to play the Snake game yourself, as the games go on, you should get better each run at anticipating.
def get_reaction_time(self):
return np.random.gamma(2, 0.05, 1)[0]This will generate reaction times that are mostly clustered around 100 ms, but with occasional longer times, simulating varied human reactions. This will still produce some superhuman reactions, so we could modify it to:
def get_reaction_time(self):
return max(0.1, np.random.gamma(2, 0.05, 1)[0])So let's build our first model. SNAIK3 Each reset, the snake will start in random direction to reduce chances of overfitting.
We will also reduce the size of the screen to make it more challenging for the snake 🐍 Now using 640x480 (32x24 blocks of 20px or a total of 768 blocks).
Let's define our criterias for success: We want our system to learn fast and slow...
To measure this, we will use a check-point system.
After 30 games
After 150 games
After 500 games
Then let it run as long as it's progressing...
Let's break down what we need:
Actions
3 directions minus the current direction
State
Snake's position & direction
Walls positions
Food location
Rewards
+10 for food
-10 for game over
Memory
Global of 100 000
Batches of 64 actions
The batches break the correlation between consecutive samples and improves learning stability. All this information is stored in binary format (1 or 0) and uses a replay function to remember and update Q values. The idea is quite simple, the "agent" will try a lot of random actions at first (this is epsilon, or exploration) then as games progress this value will go down, and it will use the highest Q value (this is exploitation) or going for the optimal move.
The first 100 runs were extruciating to watch... Basically hitting every wall, then self-collision and finally spining in circles for survival.
Game 110, Score: 2, Max Score: 2, Epsilon: 0.58
Game 111, Score: 1, Max Score: 2, Epsilon: 0.57 Then around game 500 the magic starts to show...

Game 960, Score: 17, Max Score: 52, Epsilon: 0.01
Game 961, Score: 53, Max Score: 53, Epsilon: 0.01
I kept running it for about 3000 games and it finally got to the score of 67.
Think of yourself as a kid, when playing snake on a that Nokia 3310 with 320px screen. In the initial games, you probably would have understood quite quickly the goal, yet your technique would evolve as you start playing it more. Simply put, you discovered that you had more chances of reaching a high score if you adapted your game style...
This probably involves staying away or being careful of the walls, using much longer routes to be safe and gain space, when your snake is long. 😳
Finally, as you got too close to that high score, your heart starts beating faster, and you are prone to more mistakes, yet you would try again and again. At least, I was very competitive... I remember filling about 60-70% of the screen. Which would mean a theoretical score of ~400 in the equivalent of our game. It was hard to achieve.
Credits to @GeneReddit123
The same is true for our Q-table agent, at first it tries a lot of random things and checks the outcomes (rewards/punishment) then once its epsilon is low, it only tries optimal moves according to it's training.
How could we optimize ?
Changing the game environment, we could make the snake start with 5 blocks, so that it learns faster about self-collision. Inversely, improve the game state representation by including more relevant information about the game environment like the distance to the food or all body positions.
We can tune hyper-parameters based on how long we want to run it for, how fast it's picking up on subtleties (for instance, later game state management).
self.memory = deque(maxlen=100000)self.gamma = 0.95 # discount rateself.epsilon = 1.0 # exploration rateself.epsilon_min = 0.01 self.epsilon_decay = 0.995 self.learning_rate = 0.001-------
agent = DQNAgent(11, 3) ### STATE, ACTIONS(4-CURRENT DIRECTION)batch_size = 64 ## USED TO RETRAIN ON EXPERIENCESSo this approach is called a "tabular" approach. Simply because it returns an empty dictionary which is used to store state-action values. See bellow:
def build_model(self): return {}self.model[state][action] = (1-self.learning_rate) * self.model[state][action] + self.learning_rate * targetEpsilon decay?
Think of it as learning how to cook. First you're trying a lot of recipes and techniques, as you get better you are able to combine this knowledge with new inspiration.
Adjusting epsilon decay based on how long we want to train the agent for: Say we wanted instead of just running it for 1000 games to run it for much longer... We can use a simple formulae to calculate our target epsilon after X games.
Let's say that number is 30 000 games.
Target epsilon formulae = Initial epsilon * (decay rate)^number of games
0.1 = 1 * (0.9999)^n
n = log(0.1) / log(0.9999) ≈ 23,025 games
This would leave ~7000 games with 0.1 exploration. Potentially leaving time for the agent to beat our record in that time.
Learning rate?
Think of learning rate as how quickly you adapt to feedback. If it's high your extremely sensitive to feedback, if it's low you are more stubborn.
Gamma (discount factor) ?
Think of this as how much you value the future rewards. A high gamma is like saving money for college instead of spending it now. While a low gamma, is spending it all on hookers and in the casino.
So to summarise...
Spends most of high school trying different activities (slow epsilon decay).
Gradually refines their interests and skills (decreasing learning rate).
Always considers how their choices affect their future (high gamma).
target = reward + self.gamma * np.amax(self.model[next_state]) # ^^This line uses gamma to consider future rewards self.model[state][action] = (1-self.learning_rate) * self.model[state][action] + self.learning_rate * target # ^^This line applies the learning rate to update the modelMemory?
Like we mentioned above, we use a tuple of a max length of 100 000. When I first saw this number, I thought my computer was going to explode.
But what actually is cool is that the tuple has this max length for this specific reason. We can almost know exactly how much size it will take even when full (and it deletes automatically!)
Memory Structure: Each item in the memory is a tuple: (state, action, reward, next_state, done)
state and next_state are numpy arrays of 11 integers
action is a single integer (0, 1 or 2)
reward is a float (-10 or +10)
done is a boolean (1 or 0)
Approximate Size per Item:
Each state/next_state: 11 integers * 4 bytes ≈ 44 bytes
Action: 4 bytes
Reward: 8 bytes
Done: 1 byte
Tuple overhead: ≈ 56 bytes Total per item: ≈ 44 * 2 + 4 + 8 + 1 + 56 = 157 bytes
Total Memory Size: 157 bytes * 100,000 items ≈ 15.7 MB
If you're not familiar with this each 1 byte = 8 bits
In memory, it will look something like this (illustrative):
[0,1,0,0,1,0,0,1,0,0,1] | 1 | 10.0 | [0,0,1,0,1,0,0,0,1,0,1] | False(----Current State----)|Action|Reward| (----Next State----) |Game Over?If an average game lasts 100 moves, our memory can store detailed information from 6,369 full games (100,000 / 157). Unfortunately it means we will need to increase it's memory by a lot if we want to get to a higher score.
For example int64 can represent integers from: -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807
While int8: -128 to 127. But 64 in our case, would take 8 times the space without any gain as our state representation is quite simple.
I'm lingering on this memory subject for a simple reason, I used to get a lot of errors when coding this because I didn't have the basics. It would create different data types for each state representation, that would be hard to handle in our models.
Final thoughts for SNAIK3:
Hyper-parameters are very sensitive, and each time you modify them you then have to let it run for a long time to see if it improved or not using benchmarks and visualisation. The main issue being that sometimes it can, not improve in the short run but pick up complexities later on... Meaning it's quite hard to judge early and takes A LOT of computational resources plus time.

Another powerful technique lies in incremental learning. For example, we can first represent in the state only the danger of the outside walls....
See example here.
We can also retrain the model based on the best and worst runs, which can potentially help to stabilize the system. This is called prioritized replay.
Now let's create SNAIK4.
This will follow more or less the same approach but use a neural network. This means that between our input (state) and output (actions) we will have 2 ReLu layers of 256 neurons each. While most maths in neural networks are very complex, one thing is quite simple linear activation. f(x) = max(0, x)
This basically is like a light dimmer, it cannot accept any negative numbers but accepts all other positive values.
ReLU(Σ(inputs * weights) + bias)
Inputs is our state: distance to walls, food position, etc
Weights is importance of the that input.
Bias is the threshold for activation of a neuron.
So we multiply each input by it's weight, add the bias and finally apply the activation function (the formulae above).
The network starts with random weights and biases. As it plays we assign rewards/punishments so that it can adjust these.
This introduces non-linearity, in two ways, first the ReLu cancels out negatives like we explained, which makes it so, it can kind of ignores them and focus on other positive relationships and secondly, we have another ReLu layer that can hopefully identify, more complex behaviours (like not trapping itself) which we were missing in our first model.
Mean?
This is a metric that is often used to measure an agent's performance, the idea being that you can get a feel for the last 100 games game's score and each new game, we can update this number to get an idea if it's evolving or regressing. You can decide how you want to calculate this, I decided to do the mean on all games and reprint it each run.
What is so important about this metric is that we can see sustained progress. It doesn't matter the results of a single run but instead a continuity of small experiences.
Why are Neural Networks so powerful ?
Let's break it down.
Between input layer (state) and first hidden layer: 17 * 256 = 4,352
Between first hidden layer (256) and second hidden layer (256) : 256 * 256 = 65,536
Between second hidden layer (256) and output layer (3): 256 * 3 = 768
Total connections = 4,352 + 65,536 + 768 = 70,656
So while the original number of 256 seemed low... Since our game field is barely 768 blocks, it might be totally overkill.
17 -> 256 -> 256 -> 128 -> 3
Gradual reduction in layer size, which can help in distilling important features
Again with the trade-off which is either overfitting. The best architecture can only be determined through experimentation... For example, you could also try large reduction 1024 -> 128.
Reversed architectures that decrease in size, like 17 -> 128 -> 1024 -> 3.
Man in the middle: 17 -> 256 -> 64 -> 256 -> 3.
Combining both concepts: You could even have something like 17 -> 64 -> 256 -> 64 -> 256 -> 3, which expands, contracts, and expands again.
Ladder: 17 -> 128 -> 256 -> 512 -> 3
Let's not forget you can combine them at inference, this is term referred to when done training and using in "production". Since you can save each version, you can also combine them.
There are advantages and disadvantages to different networks and here is why...
A smaller network might learn basic strategies quickly, but could struggle with more advanced tactics that a larger network might discover. In our environment the issue, towards the end, would be space management, as it's the most complicated part of the snake game. A bigger network will take more time and might acutally sometimes regress during training (at least I found it was more frequent in early stages).
For super complex tasks you could set-up 4 layers of 2048 and dueled with a second one.
The limit becomes your computer... Or supercomputer!
A 2000$ graphics cards comes in handy! Would handle a 32 million network size quite comfortably, but maybe not that notebook you got lying around.
The world's best supercomputer could theoretically handle an AI 'brain' with over a quadrillion (that's a million billion) connections. To put this in perspective, if each connection were a grain of sand, this would be enough to cover the entire surface of the Earth several times over.
Training this massive AI would be incredibly fast - it could process millions of examples in just about half an hour.
The solutions
In machine learning the problem is the solution. It can be an annoying iterative process of tuning settings but how we perceive a mistake, as an immediate negative... Here could take a couple more tries, but then finds the optimal move.
Which for us is hard because we simply think "I shouldn't have done that" and never play the game again in the next 15 years... It can be annoying to see a machine do the same mistake 100x yet, that is exactly how at one point there can be breakthroughs, where the network understands the next complexity.
In our agent, without teaching it specifically or hard-coding it in the system... It finally understands to take longer routes to better guard it's total space available and risks of trapping itself. It also starts "wiggle" to reduce the total space used.
What will do is determine a threshold for which the state should change. From early game which is quite simple, to a more complex second state. We will also adjust the reward system so that it considers staying alive (when past X food) just as important as eating more.
if self.is_collision() or self.frame_iteration > 100 * len(self.snake):
game_over = True
reward = -10
return reward, game_over, self.scoreThis first part punished the snake for any collision and speeds up training by making it so that it has limited time to eat (but more time later on with the *length of the snake).
if self.head == self.food:
self.score += 1
reward = 10 + len(self.snake) * 0.2 #SCALE
self._place_food()This rewards scales more as the length grows. Then punishes it when not eating but only by a minimal amount.
else:
self.snake.pop()
reward = -0.1 + (len(self.snake) - 3) * 0.02 #SCALEThere are several ways you can go about this.
This is like telling the system that it's okay to game over, as long as you tried surviving and it's better to eat several food than just individual units.
This prefaces a considerable change in our agent's behaviour because it will value survival so much more than simple +/- rewards. It starts kind of spinning on itself, which is a positive sign in our case, as we know that space management is the hardest part of the game.
It also makes training a whole lot longer...
The other thing that had positive impact was adjusting the minimum epsilon, this essentially is like your margin for error (and learning!). The first time I trained the network I used 0.01 which leaves too little random actions for the network to keep learning later on.
I then set it to 0.0731 which meant it was trying new moves about 7% of the time.
This can alter our mean scores slightly because well, it is more prone to errors now, yet the long term results of training, could also benefit from such a setting.
One last time, imagine yourself playing the game as a kid, if you were to hit 99% of moves perfectly, it would be slightly unrealistic, but you also would never really correct yourself after a mistake. I changed this value to 0.05 meaning 1 in every 20 moves or 95% of exploitation.
We think of this not as a mistake, but a way to make the network more responsive as there are no negative experiences in the end, it's exploration. Only opportunities to learn more complex strategies.
Often in training such systems, you will have to find a way to properly segment training. In this case, the later game stages require much more careful consideration. From the basics to not trapping itself, to managing space correctly.
The real scaling is often endured in memory and the reward system, as we established before we have scaled both survival and food with length of the snake which enables memory to understand this positive relationship. The other factor we could play around with, is both sample batch sizes of memory (how many are processed together) and the total length of the memory.
4 or 3 actions output ?
When looking online at other Snake AI projects, I found a lot of them to have 4 action space which I found odd as the game cannot actually have 4 controls. You would then have to hard-code opposing direction. The truth is in the real game you cannot press the button of the current direction, as that would simply do nothing.
While spatial information is important in 4 directions or even 8 with diagonals, there was no need for 4 actions output. If anything it would make the network less efficient 25% of the time.
Lazy & impatient
It's much more fun to see you agent beating itself often than slowly learning... Yet both have their advantages. The longer session could potentially learn much more complex behaviour later-on, but the "quick-and-dirty" approach makes it that much more appealing to code and train...
So tweak after tweak, you are hoping to get it perfect. Where it keeps increasing both it's mean scores and high score every few games.
The key idea behind Dueling DQN is to separate the estimation of the state value and the action advantages. This separation allows the network to learn which states are valuable, without having to learn the effect of every action for each state.
value = self.value_stream(x)advantages = self.advantage_stream(x)return value + (advantages - advantages.mean())And:
next_actions = self.model(next_states).max(1)[1].unsqueeze(1)max_next_q_values = self.target_model(next_states).gather(1, next_actions).squeeze(1)target_q_values = rewards + (1 - dones) * self.gamma * max_next_q_valuesThe loss function used is Mean Squared Error (MSE) between the current Q-values and the target Q-values:
L = 1/N * Σ(Q_target - Q_current)^2
Where N is the batch size.
There are so many different techniques for the most important parameters, that it makes everything a bit confusing... Googling about epsilon techniques will get you into scientific papers and complicated math quite quick.
Worse, that's just one strategy and there are hundreds to stabilize learning. Some notables ones are Noisy, Boltzmann, Parameter Noise, Mutations, etc...
I must have saved and tested 100 pieces of code before I could see magic. The first ting was changing the network structure, which probably produced the most results, for the Snake game the state representation is most important, meaning that our first layer should probably be the largest.
Common tactics that yield results
Being impatient of beating the next high score, my idea was that at some point you hit the magic settings, you figured out the optimal way to train late game strategy without hard-coding it like in our first models.
This is interesting because the system found out what took you a while, in a short amount of time. Let's not forget how many Nokia phones you ended up playing with. If you put your total playtime in comparison for your highscores, the machine has learnt that in a fraction of the time (although a lot more intensly).
Even though training can take several thousands of iterations, we can keep trusting the network as it's still exploring better solutions at our minimal epsilon. This means that effectively it is still trying new moves, whist being optimal most of the time. As long as we see our mean scores generally moving in the right direction, we can assume the network has not hit local optima or that training is effective.
This run used a very quick epsilon decay meaning after 30 games our network was only learning 1% of the time. Yet what was impressive is the sheer speed at which it learned to play the basics.
Speed x4 early games. After 25 short games, reaching 30+ scores. 85 @ 493
I then let it run for much longer but only for marginal improvements.
Game 2232, Score: 71, Mean Score: 37.67, Max Score: 96, Epsilon: 0.01
Game 2233, Score: 37, Mean Score: 37.92, Max Score: 96, Epsilon: 0.01
Game 2234, Score: 75, Mean Score: 38.62, Max Score: 96, Epsilon: 0.01
Best of both worlds.
My next idea was at some point, you coupled the rewards scaling and the training epsilon resets, so that we avoid hitting a plateau, maintining learning in later stages. How we can try to achieve this is through the monitoring of the mean scores.
Say you were playing the game, and at some point you notice that you are not making significant progress anymore, you would need a way to reset and try new things.... Again the same is true to our NN, as soon as it gets stuck in a certain score range, we will tell it to try be bolder about trying new things. Hopefully this makes it so that our local optima is much higher.
For example, we can use mean scores to check for regression and encourage more exploration or inversly when seeing a lot of progress!
I was stuck at 90~ and a mean of 40~.
I could have probably done better with a bit more tweaking of epsilon, learning rate and state representation but I started getting bored.
The agent might learn a strategy that works reasonably well (like following walls)
This strategy is a local optimum - better than random movement, but far from the best possible play. As playing close to walls also closes off more space.

State rep: An accurate and comprehensive state representation is critical. This layer needs to capture all relevant information about the game state.
I had to modify this several times. You can probably do it better than I did.
I want it to accuratly depict how it all ties together and the NN structure. Here's a conceptual diagram of our arborescence >
It also clearly shows both the flow and the seperation of Advantages & State values.
Now to give you an even better view of what is happening in real time. On the left you can see the input values (distance to walls, food, snake positions, etc) on the right the outputs (right, left of forward) and in the middle it's illustrative as there are a lot more connections (hidden layers).
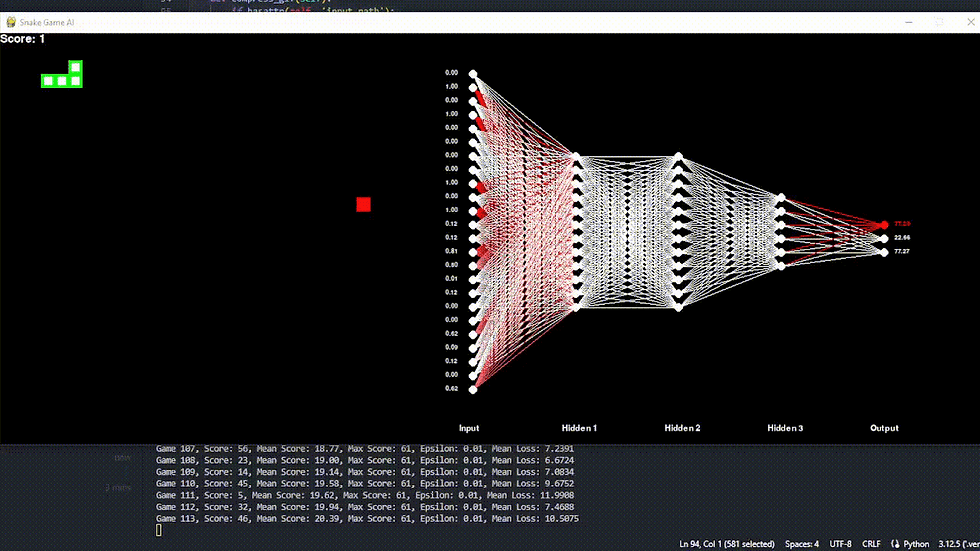
Loss?
Loss is the difference between the predicted Q-values (which estimate the long-term reward from taking an action in a given state) and the actual target Q-values (what the agent should have learned based on its experiences).
(loss = (current_q_values - target_q_values).pow(2) * weights)We use power of 2 so that it's always positive and that small rewards are less amplified than large ones.
In the image above, the loss is quite high (around 10) meaning that there is a large difference between predicted outcomes and actual rewards. Basically everything in our model is affected by this, and that probably is why we are not getting past the 96 score.
target_q_values = rewards + (1 - dones) * self.gamma * max_next_q_valuesSince our Q values are shaped by our rewards, state, and gamma. We can look for issues there.
It's normal for this number to fluctuate slightly but large spikes or large numerical values are never really a good sign. The lower the loss, the more likely your system is understanding it's environment. It's okay for loss to be higher during the initial phases of training but should stabilize at lower values later-on.
Let's wrap this up with SNAIK5.
Since I'm lazy and couldn't figure out a proper system, for all of the above, we are going to use genetic modeling or some weird complicated techniques to beat our previous scores.
There is also a suite of other settings I won't get into details about (alpha & beta & scheduling)... But then I thought, we can just use genetic algorithms to find the best settings for us. Then use crossover and mutation to self-optimize (parent to child), it even goes as far as changing the size and shape of our NN.
Genetic algos are a bit like battle-royale. You have a starting population, then it is survival of the fittest. Create the next generation, add mutation and cross-over, rince and repeat for many generations.
Now hopefully our new way of handling hyper-parameters creates some super-monster, we barely understand. Generally, it gave me good indications of what I should modify, to push further my original code.
We start with a diverse group of 40 AI agents, each with its own unique set of characteristics - things like how quickly it learns, how often it explores new strategies, and how its brain (neural network) is structured.
This is what a single agent's output will look like:
Generation 1, Agent 1, Episode 78: Score = 12And at the end of the 500 games of the 40 agents we get another output:
Generation 1Best Fitness: 15.10Average Fitness: 6.96Top Score This Generation: 18All-Time Top Score: 18 (Generation 1)Best Agent Epsilon: 0.0178Best Agent Learning Rate: 0.000725Best Agent Hidden Sizes: [229, 136, 174]After this it's the next generation's turn. We take the best-performing AIs and use them as "parents" to create the next generation. We mix and match the characteristics of successful AIs, and even introduce small random changes (mutations) to potentially discover even better configurations.
This process repeats for 2000 generations. With each new generation, we hope to see AIs that are better at playing Snake than their predecessors. The beauty of this approach is that it can discover strategies and configurations that we might never have thought of ourselves.
Realistically this will play 40,000,000 games of Snake.
Which would be an issue... First it would take a horrible amount of time and second my computer would not enjoy it. Obviously there are solutions to this. We can run several instances at the same time, we can remove the rendering of the game, this is called "headless". So that's exactly what we are going to do.

Okay maybe 40 agents was a bit optimistic. Let's run 5 snakes, they'll be a little more inbred...
Now it's the settings roulette:
def initialize_population(self): for _ in range(self.population_size): hyperparams = { 'gamma': random.uniform(0.9, 0.999), 'epsilon': random.uniform(0.1, 1), 'epsilon_min': random.uniform(0.01, 0.1), 'epsilon_decay': random.uniform(0.99, 0.9999), 'learning_rate': random.uniform(0.0001, 0.01), 'update_target_frequency': random.randint(10, 1000), 'hidden_sizes': [random.randint(64, 256) for _ in range(random.randint(2, 3))], 'priority_alpha': random.uniform(0.4, 0.8), 'priority_beta': random.uniform(0.3, 0.7), 'priority_beta_increment': random.uniform(0.0001, 0.001)If this doesn't beat 96 score, well... I will have to copy paste the first code that comes up on GitHub. Then, magic happened again... 3rd generation 2nd run got to 55 score. In two runs!
I had to change the state rep one last time to include more relevant information. Then I was basically sure to have improved the code so much that it would not only do well, but do almost perfect.
Behold the inbred Snake Olympics.
The genetic algorithm pointed towards a larger first layer, maitining epsilon and learning rate quite high for late game which makes sense.
Reseting epsilon periodically
# IN THE CLASS self.reset_epsilon = 0.33if self.epsilon > self.epsilon_min: self.epsilon *= self.epsilon_decay self.steps += 1 # Reset epsilon every X steps if self.steps % 10000 == 0: self.epsilon = self.reset_epsilonAnd then the better way is to decrease this reset over time:
reset_epsilon = max(self.reset_epsilon * (1 - self.steps / 1000000), self.epsilon_min)First 100 games example data.

This introduces two things: Forces the network every ~25 games to reset the amount of random moves %. Again increasing flexibility but at the cost of loss being higher.
A better way to handle this is with the current score. We can, for example, reset the epsilon at 50 and 75 etc.
We can notice the loss is increasing meaning that we either didn't scale the rewards properly or the state rep is not descriptive enough. More on that later.
Now hopefully because of genetic modeling we know the best settings, we also have some kind of mechanism to reset the randomness (and we could do the same for learning rate). We are just missing one small piece which is retraining on best runs or proper priority replay.
I also thought why not try do it manually (with arrow keys or something) would be fun. See it's struggling, no problem, increase learning and epsilon, fixed? Or reduce again.
You need a way to store the best runs and to retrain your agent based on this data. Which isn't necessarily straight-forward as you now have to have two memories, and two training methods.
You might be asking yourself why is he doing this for this game? Well you could apply the same principles to remotely any problem... The more complex, the more state representation and network structure.
Everything Algorithms
In the first part of this blog post, we discussed the BFS algorithm as implemented in SNAIK2 and how it could essentially hard-code a win for most Snake game scenarios. This approach highlights a fundamental principle in computer science and artificial intelligence: the power of breaking down complex problems into more manageable sub-problems.
The definition of an algorithm, at its core, is a step-by-step procedure for solving a problem or accomplishing a task. What's particularly interesting is how this concept of problem decomposition applies not just to specific algorithms like BFS, but to the broader field of AI and problem-solving in general.
This method of problem decomposition scales well beyond simple games. In more complex AI systems, breaking down problems is crucial for tackling challenges that would be insurmountable if approached holistically.
For machine learning the same is true, complex tasks are often broken down into a series of simpler mathematical operations. Neural networks, for instance, break down complex pattern recognition tasks into layers of simpler computations.
While fractionning is powerful, it's important to note that not all problems decompose neatly. Some challenges require considering the system as a whole, then when you think you have the full picture there are more factors to consider. This is particularly true in complex, dynamic systems like financial markets, ecosystems, or social networks.
Say your algorithm or neural network was to trade stocks for you... Well then it would be a whole different ball game, and you wouldn't want to go broke...
The stock market is influenced by countless interconnected factors - economic indicators, geopolitical events, company performance, market sentiment, and even seemingly unrelated events that can cause butterfly effects throughout the system, see more recently GME stocks or even crypto-currencies. Based on the data provided from Crédit Suisse a reasonable estimate for the percentage of algorithmic trading in the stock market is 60%+.
In such a complex environment, we might miss crucial interactions and emergent behaviors. A purely reductionist approach could overlook important systemic risks or fail to capture the nuanced ways in which different factors influence each other.
As more traders use similar algorithms, the market dynamics shift, potentially rendering the original strategy less effective. This self-referential aspect of financial markets adds another layer of complexity that resists simple decomposition. This was especially true for scalping (very fast trades that used split second reactions to make profit), where it became a competition of how fast and low fees your trades could have.
For instance, a stock trading algorithm might use neural networks to analyze individual stocks and sectors, but also incorporate higher-level models that consider market-wide trends, sentiment analysis, and even game theory to account for the actions of other market participants... Good luck!
What makes a system good?
This provides balance between short-term analysis and a wider state based "brain". This is a common phenomena in machine learning, reduction vs. hollistic approaches.
Another term that is often referred to is "heuristics". Accordding to Oxford definition in Computing: Proceeding to a solution by trial and error or by rules that are only loosely defined.
In essence, heuristics are mental shortcuts or rules of thumb that help us make decisions efficiently, yet they might not be optimal, but is sufficient for reaching an immediate, short-term goal or approximation.
Like me coding to get to 25 score, then 50, instead of directly doing it properly...
To illustrate this principle I will use AlphaGo as an example. The medium is a complex game, we don't really need to understand.
To me the most intresting part is that, human commentators were shocked at some moves that felt sub-optimal, but actually were probably close to perfect statistically speaking.
This highlights a key aspect of AlphaGo's achievement: it was able to identify strategies that were statistically optimal, but counter-intuitive to human intuition, even for top players.
Our experience and intuition can lead us to oversimplification and biases. So while the commentors (who are probably avid players) thought "Wow, this is illogical." The best player in the world quickly realized that while that move felt odd, he was doomed, as it was statistically perfect.
This is the results of deep learning, data-driven approaches that can help us discover novel solutions and/or challenge our preconceived perceptions, but can also reduce something to plain simplicty.
We might decide to play a game agressively or defensively based on our opponent, yet optimally it might have been a mix of both, and sometimes total neutrality (this was the type of moves the commentators were most surprised about).
How did they do it?
Now Google DeepMind team did reveal a little bit of what they used to make it so efficient, which we can look into... First is the Monte-Carlo Tree Search, this algorithm excels in large spaces, by focusing on positive relationships with child nodes. Basically finding the optimal paths instead of searching all possible moves. This is hollistics to reduction or heuristics.
Then it was trained on human gameplay with deep neural networks. This is hollistics, as we know deep neural networks are more powerful, the more data they are provided with (quality and quantity checked).
Some more techiques include, reinforcement, transfer and self-play learning. Then, with enough time and computational resources, we eventually get to an optima, there is no more competition but itself or the next iteration of code improvements.
While the rules of the game are fixed, the optimal strategies that the system can uncover are not. As the AI trains and refines its approach, it may discover new patterns or strategies that challenge what we consider: "optimal".
The only available benchmarks during training are either human expertise or the AI's own prior performance in self-play. However, these benchmarks may not always reflect the true global optimum, especially when considering the long-term versus short-term advantages of certain moves.
In other words, the optimal pathways to victory are not static—they are constantly evolving based on the game state, the AI's learning, and its ongoing analysis of new situations. Even though the rules of Go don't change, the strategies that work best in the game can vary dramatically depending on the specific circumstances and timing of moves.
A humorous example from the SNAIK illustrates this: when the survival reward is set too high, the snake can find a way to effectively "game" the system. Instead of actively seeking out food, it might settle into a predictable, repetitive pattern—like moving back and forth between the top and bottom of the screen or left to right—basically not playing or avoiding danger at all costs by not turning but only at the walls and covering the whole screen one block per one block. In this scenario, the snake can essentially live indefinitely, prioritizing survival over actual "gameplay".
This is also well pictured by the sigmoid S shaped curve.
This function which is found everywhere, provides a useful analogy for how the progress of such systems like AlphaGo evolve decision-making in complex environments. The sigmoid function captures a fundamental tension in decision-making: it allows for non-linearity. Small changes in input (board position, move sequences) can produce small or large changes in the outcome, depending on where you are on the curve.
It also emcompasses a similar concept that can be applied to human learning and expertise. When we first learn a skill, we improve quickly. As we become more advanced, we find it harder to make big leaps in performance. Greater effort, for little improvements and the same is true for any system.
AlphaGo was pushing beyond the human benchmark, but even for AI, there might still be strategies it hasn't uncovered. The plateau in performance doesn't necessarily indicate that the system has reached the true global optimum—it may simply have exhausted the capacity of the current system to find better strategies, given the data and computational resources available.
When the system began making moves that defied human intuition, it was operating in an area beyond the plateau of human expertise, where it found moves that were statistically optimal but challenging for even the most experienced human players to grasp.
Imagine rebuilding the same AI two years after these discoveries were made. Well it probably would shape new refined strategies based on the adapted gameplay of the first iteration, as human players adpated their gameplay, perhaps the system would become more aggressive or defensive, reflecting these evolved dynamics?
Chess & Poker
This was observed with the rise of solvers for Chess and Poker (which are more popular than some people think) what happened is that it was so commonly used on large available datasets, that at some point, the same original system starts adapting to other people using solvers (some good and bad ones).
In poker, solvers have led to a rise in what's called "GTO" (Game Theory Optimal) play, where players aim to make moves that are unexploitable over the long run. However, this has also led to counter-strategies from players who recognize common solver-based tendencies.
Example of pre-flop table for games of "all-in or fold" with 4 players. Based on large amounts of data.
Data never lies
The system would all-in a pair of 2 in-hand (in 4 player game of all-in or fold), which might seem ridiculous at first, but again is statistically sound. Pockets 2s are a made hand, meaning you already beat high-card, and the expected value of this hand is about 15% chance of winning. Might seem low but really is quite high, then you have 11.76% chance of at least one other 2.
The system isn’t just hoping to get lucky; it’s playing the odds based on long-term expected value. Your 15% chance of winning accounts for both favorable and unfavorable situations. Against higher pairs like 77, 88, or even something as high as AA, well you're f'ed. But against unpaired hands (which will often be in the mix), you have a much better chance.
Say only one person all-in's with you, Ace-high hand (like A♣K♦, who wouldn't all-in with this??) your pocket 22s are actually slightly ahead:
AK wins: 812,340 / 1,712,304 ≈ 0.4744 or 47.44%
22 wins: 899,964 / 1,712,304 ≈ 0.5256 or 52.56%
Now if all 4 players all-in with you well let's just hope you get lucky.
This illustrates well my point that, while it might seem counter intuitive at first, the data behind is actually in favor of the system. While the other player will scratch is head when hunderds of dollars are lost to a pair of 2s.
A poker AI trained on older solver data might struggle to keep up with the latest trends because those trends are themselves, adaptations to solver strategies. Again some "way-more-aggressive" solvers started taking the upper hand recently.
This led to a new kind of "meta" in chess where certain aggressive or counter-intuitive moves became standard. The concept of continual learning becomes crucial in avoiding this kind of stagnation. Systems must be able to not only learn from new data but also adapt when the very environment they are operating in, as it changes due to their own success.
For instance, in chess, after the rise of chess engines like Stockfish and AlphaZero, human players began incorporating engine-like moves into their games. Which is definetly cheating if used in live-play but wouldn't you want to learn it's best tactics after you lost 20 games on Chess.com ...
AI is constantly chasing a moving target.
As systems continue to learn and adapt, they not only uncover novel strategies but also shift the landscape they operate in—leading to a dynamic and often unpredictable process of co-evolution between what was and what is.
This is often referred to as "Meta-learning". Instead of rigidly adhering to predefined rules, autonomous systems must balance exploration and exploitation—experimenting with new behaviors when necessary, but also knowing when to stick with tried-and-tested strategies. Here, AI must grapple with novelty detection—the ability to recognize when it encounters entirely new scenarios that it wasn’t prepared for.
This concept aligns with the notion of autopoiesis, a term from biology referring to systems capable of self-renewal and self-organization. Today we decide to what we apply such power with our creativity and intuition.
If I see one more Snake Game I will jump off a roof, so let's switch up the environment. You're still reading ? Damn that's crazy, you're a nerd.
Mazes. Just like our Snake Game, are simple yet relatively complex to do "well" in. Meaning, we can measure several metrics to compare and benchmark different algorithms and learning techniques. I stole most of the code from one of my best friends. So credits to him for the original maze generation ❤️.

Four different algorithms (DFS, BFS, A*, Djikstra) solving the maze. Small grid, which we can make much more complex.
The flickering is an interesting visual bug where the solver is actually trying several paths simultaneously, because I forgot a "break" in the code 😂
We will test them on a much bigger maze. We can then benchmark them using several criterias.
Ideal path length: 1887
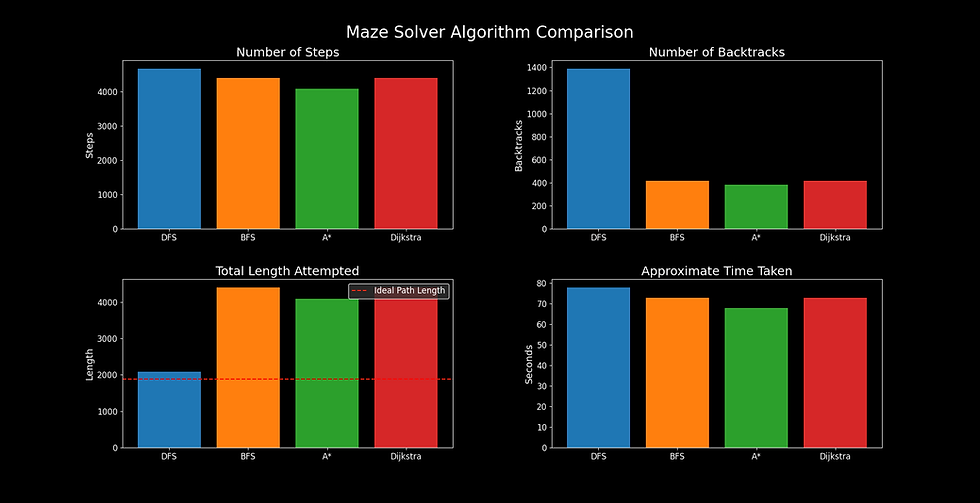
Interestingly, the trade-offs between algorithms are becoming more apparent. For example, while DFS gets closer to the ideal path length, it suffers from excessive backtracking. This makes it less efficient for larger mazes. On the other hand, A*'s consistency comes from its heuristic-driven approach, minimizing backtracking but occasionally overshooting the ideal path due to its reliance on approximations.
Let's run one algo on a much bigger maze.

Total length attempted: 4549
Ideal path length: 1759
What’s interesting to note about these algorithms, however complex, is that they’re not just used for GPS navigation or solving mazes.
In fact, their applications extend far beyond traditional pathfinding tasks. These algorithms are at the core of solving many real-world problems and so are many others.
Similarly, Dijkstra's algorithm, renowned for its precision in finding the shortest path in weighted graphs, plays a crucial role in network optimization, ensuring data packets take the most efficient routes across the internet.
The real magic of these algorithms lies in their flexibility and how they can be used to explore data structures like trees or linked lists, can help traverse hierarchical data, systematically exploring all possible combinations of features to uncover meaningful insights. The versatility of these algorithms is incredible. They’re rooted in pathfinding, but their underlying logic—exploring possibilities, optimizing solutions, and making decisions—makes them adaptable to a variety of tasks.
From sorting datasets to resource allocation and decision-making in machine learning. It’s this flexibility that makes them not just useful, but essential, in so many advanced systems today.
I know you're here for the SNAIK... Well it would have been quite easy again to juste hard-code 200+ score with such algorithms or just copy from GitHub some code... But where’s the fun in that?
There’s something uniquely satisfying about diving into the process, tweaking every little detail, and watching it evolve bit by bit—sometimes painfully slowly—over weeks of trial and error. During training you have time to read-up on best practices or how to tweak X, Y.
And there’s something deeply rewarding about this hands-on, problem-solving approach. It’s one thing to watch an algorithm flawlessly complete a task; it’s another to see your own creation grapple with the complexity of the game, slowly but surely improving. With every tweak, the AI starts to make smarter decisions, its movements becoming more efficient, and suddenly, what felt like an impossible goal—like hitting that elusive 200+ score—seems within reach.
Training runs that get to high scores hopefully teach our SNAIK to use better pathing:
Game 3896, Score: 50, Mean Score: 21.72, Max Score: 101, Epsilon: 0.32
There is also a lot of frustration, when breaking the code when changing something minor, or losing that perfect version you made because of a Windows update. It’s moments like that where the temptation to just grab someone else’s code off GitHub starts looking really appealing.
Some notable algos for this issue is flood fill, hamiltonian grid cycles, and the idea would be to give this information to machine learning model so that it can both use algorithmic data and learn from mistakes.
Tying it all together
When I initially started this project I thought it would be much easier, but everytime you dig a little more you find more small settings that can be tweaked. The last powerful technique I found was self-play with a single opponent which yields intresting results because you can benchmark your own changes, share the memory system and the scheduling by holding a competition between the two, so that it's less prone to plateauing. For example if one snake is 20% behind we reset it's learning rate and epsilon. If not, we decrease more.




Comments